This blog talks about mathematical understanding of the basic reproduction number $R_0$. $R_0$ is an important argument in viral transmission, such as COVID-19. We construct a math model and propose that $\Pr[\mathrm{Virus\ extinction}] = 1$ if $R_0<1$, and $\Pr[\mathrm{Virus\ extinction}] < 1$ if $R_0\geq 1$.

病毒基本传染数R0的数学理解

本文根据孔雨晴老师随机算法课整理撰写.

我们在关于疫情的新闻报道里经常听到$R_0$这个词，$R_0$读作R naught，英文为basic reproduction number，中文译作基本传染数，我们可以通俗的把它理解为平均每个病人能够传染的人数.

作为一篇科普文章，本文中我们首先对病毒传播进行简单的数学建模，再给出$R_0$的数学定义，最后给出$R_0$的数值和病毒灭绝概率的关系：当$R_0<1$时病毒灭绝的概率为1，而$R_0\geq 1$时病毒只以小于1的有限概率灭绝.这篇文章不是严格的数学证明，使用了大量口语表述和不严谨表述，以求没学过大学数学课程的同学也能看明白.

1 病毒传播的简单数学模型

我们可以根据生活经验，对病毒传播给出一些假设，这样我们就建立一个简易的病毒自然传播的数学模型，我们假定

1. 首先，感染病毒的人数占全球人数比例很小，因此我们模型中总人数为无穷

1. 最开始感染病毒的人很少，为了简单起见，我们可以假设最开始只有一个病人感染了病毒，我们称这个人为0号病人
2. 每一轮中，一个病毒感染者可以把病毒传播给0个人到无穷多个人，本轮传染完之后此人不再传染病毒，比如这个人被隔离了。

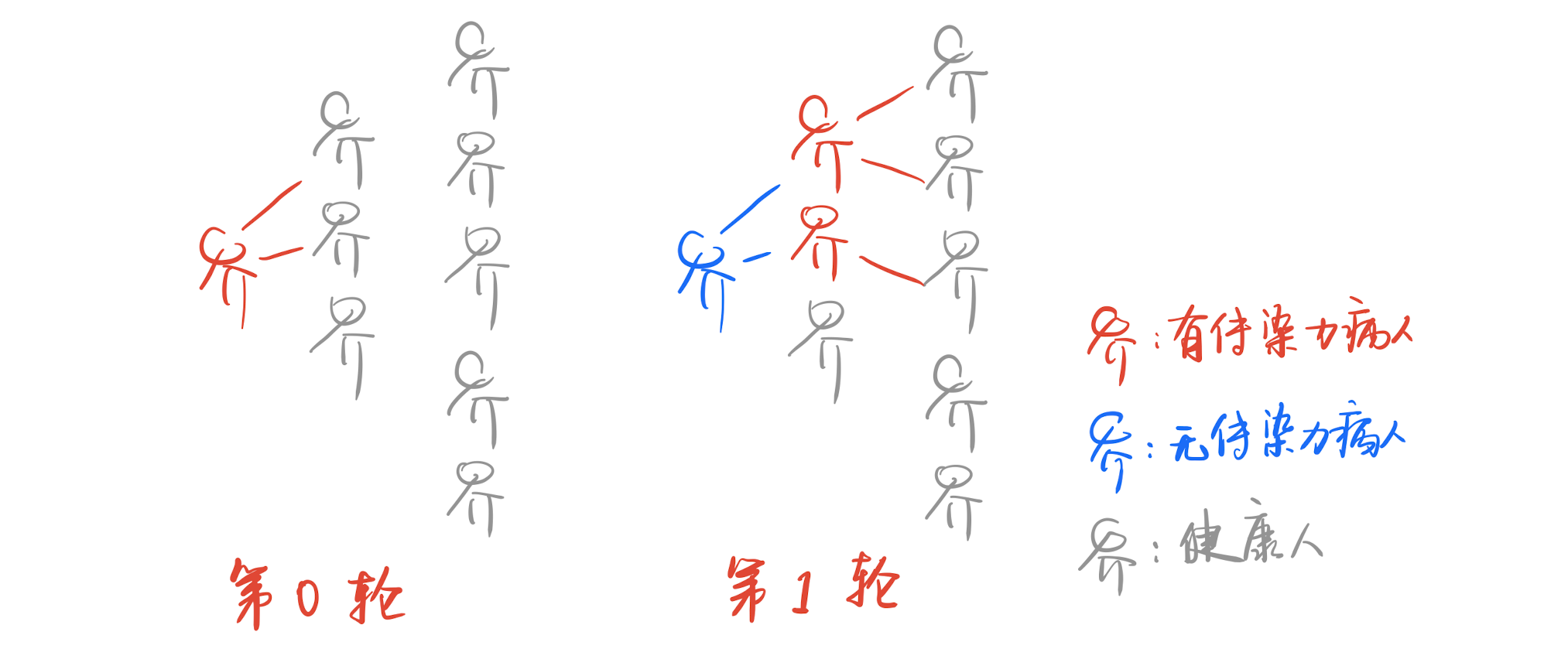
1. 一个病人可以传染的人数是随机的，但我们可以假设这个病人可以传染的人数是有一定规律的，比如有$40\%$概率传播给0个人，$30\%$的概率传播给1个人，$20\%$的概率传播给2个人……用数学语言描述这个规律，就是，一个病毒感染者可以感染的人的数量是服从分布$\mathcal D$的随机变量$Z$，即传染给$i\in [0,+\infty)$个人个概率是$\Pr_{Z\sim \mathcal D}[Z=i]$，每个病人都以这个概率继续传染别人，也就是每个病人的$\mathcal D$都相同。

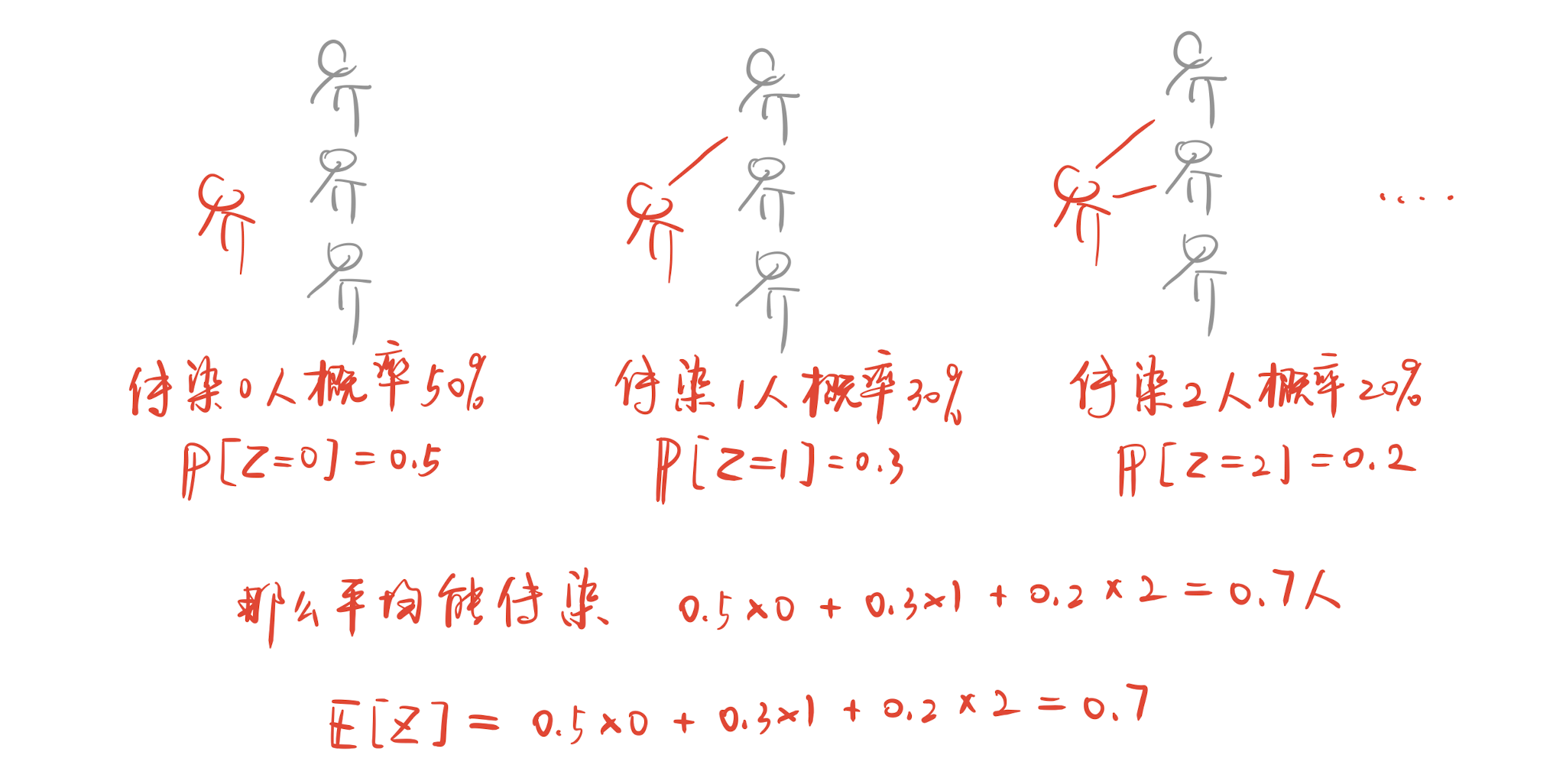
1. 每个病人可以传染的人数是随机的，满足4中的规律，但是，“平均”他能传染的人数是有限的，比如5个人，而不是无穷大。用数学语言就是，每个病人可以传染的人数的期望收敛，\(\mathbb E_{Z\sim \mathcal D}[Z]=\sum_{i=1}^{\infty}\Pr_{Z\sim \mathcal D}[Z=i]i<+\infty\)
2. 某地的0号病人可以引发一场疫情，当这些中招的人不再增加的时候，也就是病毒在某轮中不再传染到未感染的人的时候，我们就可以称由该病人引发的疫情灭绝。一场疫情可能无法灭绝，也就是病毒会永远传下去（因为我们假设人数无限），所以我们可以考虑由一个病人引发的疫情灭绝的概率。每个病人是等价的，所以我们可以假定每个人引发的疫情灭绝的概率相等，记作$p$

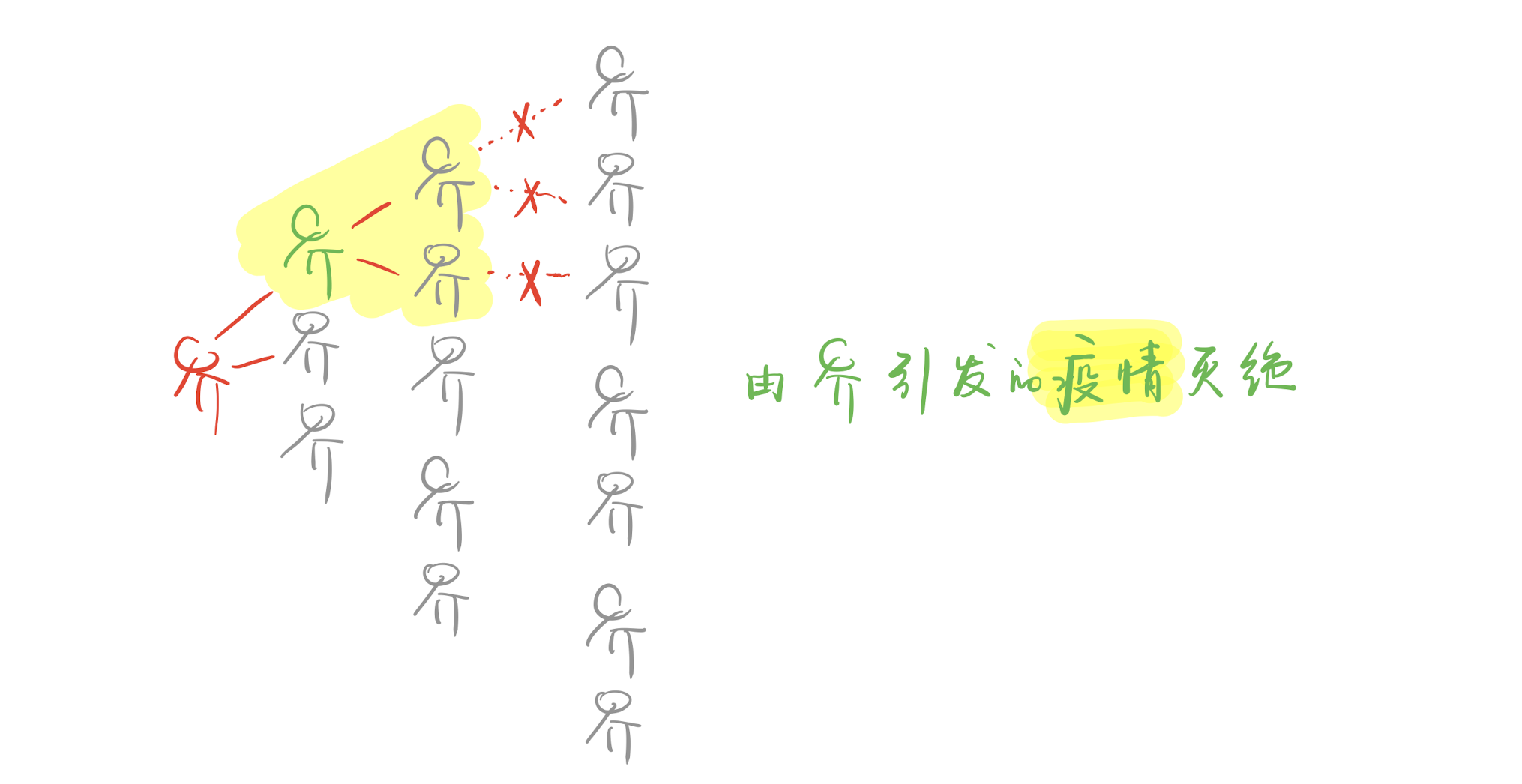
1. 整个疫情中的0号病人引发的病毒传染疫情灭绝，则病毒灭绝。如果病毒会永远传下去（比如永远共存了），那么病毒就不灭绝。整个疫情的0号病人和某个地方的0号病人是等价的，所以病毒灭绝的概率也是$p$

2 $R_0$的数学定义

我们可以把$R_0$定义为，一个病人”平均“可以传染的人数。在数学上，这种随机数的平均值可以被称为数学期望。

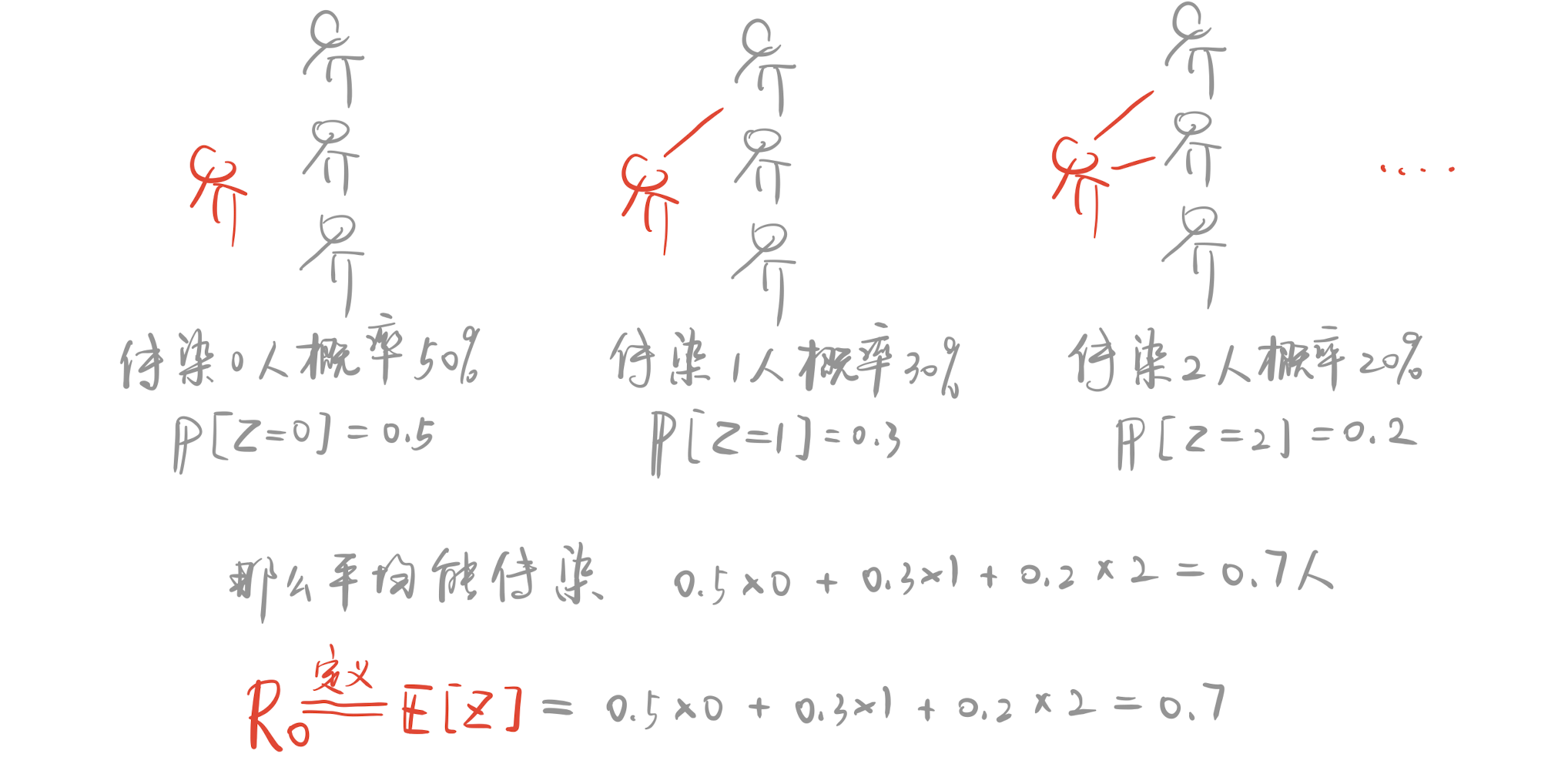
数学语言中，$R_0$定义为一个病毒传染者可以感染的人数的期望\(R_0=\mathbb E_{Z\sim \mathcal D}[Z]=\sum_{i=1}^{\infty}\Pr_{Z\sim \mathcal D}[Z=i]i\)

3 $R_0$的大小与病毒灭绝概率的关系

考虑第0号病人，我们可以计算这个人引发的疫情灭绝的概率。如果这个人有$40\%$概率传播给0个人，这种情况下病毒就概率为1地灭绝了；$30\%$的概率传播给1个人，那么这种情况下病毒有$p$的概率灭绝；$20\%$的概率传播给2个人，那这种情况下，只有这两个人引发的疫情都灭绝，整个病毒才灭绝，所以这种情况下病毒有$p\times p=p^2$的概率灭绝……我们把这些情况发生的概率，乘以该状况下的病毒灭绝概率，加在一起，就是整个病毒灭绝的概率。

\(p=\Pr_{Z\sim \mathcal D}[Z=0]+\sum_{i=1}^{\infty}\Pr_{Z\sim \mathcal D}[Z=i]p^i\) 满足这个条件的$p$就是病毒灭绝的概率.接下来我们就试图算出这个$p$.我们把这个式子的右边当作一个函数来看，定义 \(f(p)=\Pr_{Z\sim \mathcal D}[Z=0]+\sum_{i=1}^{\infty}\Pr_{Z\sim \mathcal D}[Z=i]p^i\) 则问题转化为寻找$f(p)$的不动点，也就是$f(p)$与$g(p)=p,p\in[0,1]$的交点.

我们发现，这个函数$f(p)$的图像是一个单调上升，且弯曲向下凸出的曲线，它在0到1之间（不含1）最多只能和$g(p)=p$相交一次，然后就不再相交，我们可以严格的导出这个结论，这个过程看不懂不影响结果。注意到：

1. $f(p)$是连续函数，这意味着它的图像是一个连续的直线，没有间断乱跳的点
2. $f(p)$可导，导数非负，这意味着它单调递增，是一个从0到1一路向上走的曲线
3. $f(p)$二阶导数非负，是凸函数，这意味着它弯曲的曲线向下突出
4. $f(0)=\Pr_{Z\sim \mathcal D}[Z=0]\geq 0$也就是说病人不把病毒传染给其他人的概率大于等于0，这个曲线从0或者$g(p)=p$直线的上方开始

因此，如果这个曲线在$p=1$点附近的导数$f’(1)\geq 1$那么它在$p=1$附近必然有一部分和直线$g(p)=p$重合，或者干脆在直线$g(p)=p$的下面，而这个曲线又是连续的，所以它在0到1之间（不含1）和$g(p)=p$有交点。

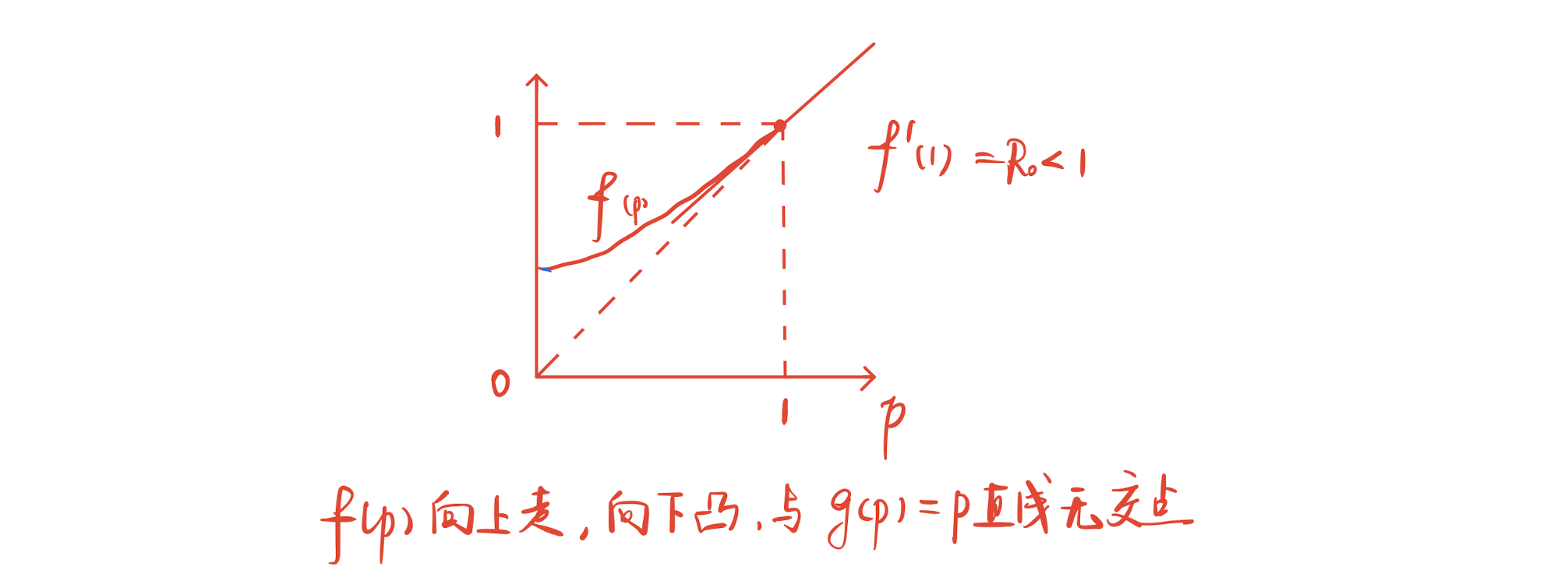
而$f’(p)<1$的时候，这个曲线在$p=1$的附近都在直线$g(p)=p$的上面，它又是往下凸出的连续上升曲线，也就是说上升的越来越快，那么从1往0看，它就和直线$g(p)=p$渐行渐远，不可能有交点了。

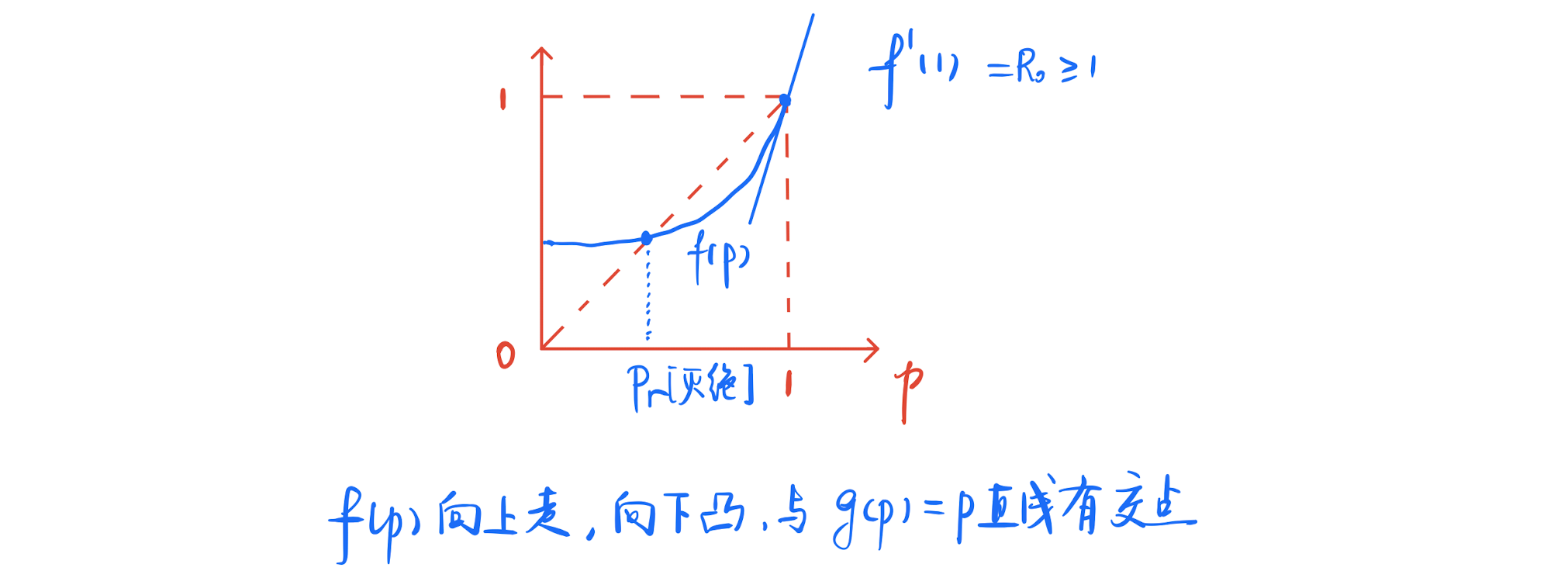严格的说，就是$f(p)$在$[0,1)$间与$g(p)=p$没有交点，当且仅当 \(f'(1)<1\)

而我们注意到，$R_0$正好等于$f(p)$在$p=1$处的导数 \(f'(1)=\sum_{i=1}^{\infty}\Pr_{Z\sim \mathcal D}[Z=i]i=\mathbb E_{Z\sim \mathcal D}[Z]=R_0\) 所以，当$R_0<1$时，$f’(1)<1$，只有$p=1$一个不动点，病毒灭绝的概率等于1；而当$R_0\geq 1$时，存在$p<1$的不动点，病毒只以小于1的概率灭绝

我们得到结论，当$R_0<1$时，病毒灭绝的概率等于1；而当$R_0\geq 1$时，病毒只以小于1的概率灭绝